[mashshare]
Bob Alejo called me up and said, “Hey B, what’s new? Or should I say, what’s new with VBT? I want another article on it.” There are a couple of things that I’ve been doing: the first with force-velocity profiling and the second with creating load-velocity profiles and assembling zones on exercises out of the norm.
Force-velocity profiling is nothing new. I assure you that in 1983, when the Kaneko study1 that I will reference later came out, it wasn’t truly new either. But before we go any further, I think we need to take a minute and differentiate between some terms, as there seems to be some confusion.
Load, force, velocity, acceleration, and power. I have seen some people talking about acceleration when they really mean power (I know because their unit was watts) or velocity (because the unit was m/s and not m/s2). I have seen some people saying force when they are really talking about load (I know because the unit was kg and not N).
Load is simply the weight that is being lifted. It can be expressed as an absolute load (how much weight is being moved) or a relative (sometimes called normalized) load (percent of 1RM). For instance, let’s say that I have a 200kg squat max, and I’m supposed to lift 60% of that. My absolute load would be 120 kilograms and my relative load would be 60%.
Acceleration is the change in distance per unit of time squared, and velocity is distance per unit of time. If I were to run a 10-meter sprint with a time of 1.65, my velocity would be calculated as 10/1.65, equaling a velocity of 6.06 m/s. My acceleration would be calculated as 10/1.652 = 3.67 m/s2. The point is that these are two different units, and even over the same distance with the same time they will yield two different scores. Thus, they are not interchangeable, as some people seem to believe.
Force is mass times acceleration (some try to calculate it as mass times velocity, and this is not correct), as Isaac Newton’s second law tells us. (F=ma is the common representation.) So, whatever the mass being lifted, if you multiply it by the acceleration, that derives Newtons.
Power is force times velocity. While force mathematically is more dominated by mass, power can be more dominated by velocity. Because of this, it is important to know how peak power was derived. Meaning, looking at not only what power was, but what was the mass and what was the velocity.
It is important to know how peak power was derived. Meaning, looking at not only what power was, but what was the mass and the velocity, says @jbryanmann. Share on XLet’s say the power was 500W. Was it a 500N force and a 1m/s velocity? Was it a 1N force and a 500m/s velocity? Was it a 25N force and a 20m/s velocity? While we are looking at some extremes on this example, the point is that force and velocity are players. Someone could be more toward one end or the other, and if we examine where it occurs, we may need to alter training to move it. If power is occurring too late (i.e., post 200 or 250 ms), then we can see this and change training to use things that are lighter and faster in order to alter training to elicit power to occur sooner.
I’ve said it before and I’ll say it again: If you want a new idea, read an old book. Sometimes it’s just an old study, but either way it gets the job done. I was sitting in on a class taught by Dr. Joseph Signorile, who is nearly infamous for his work on power training with aging and diseased populations. He happened to show that 1983 paper by Kaneko1 that I mentioned before, and it hit me. If I just change up a small amount of what we do for a 1RM test, we can do force-velocity profiles and gain so much information on what the athlete can do and what the athlete needs to do to improve.
Take Your 1RM to the Next Level
If you are using a GymAware or another device that accurately gives force, velocity, and power at every load, you can easily figure this out. Also, from personal experience, you can set up the GymAware to plot these things for you, so this is why I specifically mention this device. I’m unsure of the others. It will require some alterations to the typical testing of the 1RM.
With the 1RM, you are approaching true maximal force capabilities, so the force end of the spectrum is well controlled. However, most people start out at around 60% of 1RM after the warm-ups, and rightly so as this is mentioned in most protocols as a good starting point. However, this won’t give the maximal velocity component to see how the athlete is here.
I recommend starting with a ballistic version of the exercise for 3-6 repetitions with either a PVC pipe or a wooden dowel to get an unloaded condition to get a maximal velocity, and then a ballistic with 20% and possibly 40 % of 1RM as well to get a well-plotted curve as we move into the mid-range with the 60% of 1RM starting point. If I perform 1-3 sets that have minimal load and require minimal rest, I tack on probably 2-3 minutes of training time, but I gain a greater insight into the way the athlete performs.
During all of these sets, from the unloaded ballistics all the way to the 1RM, velocity, power, and force need to be recorded from the device and then plotted. You can use Excel (but it does get tricky), SigmaPlot (I prefer this one, but I only use it because we have it at Miami), and I have heard you can even do it in R and other software that is used for visualization like Tableau, but I cannot confirm this. When examining force and velocity, you will see that the relationship is curvilinear rather than linear. (Force rather than load is being utilized. Load-velocity is a straight(ish) line).
Once you see where the athlete excels, where they are deficient, and where power occurs, you can attempt to develop the appropriate force or velocity end of the spectrum, or a mix of both. If you examine the different loads as presented in Figure 2 of Kaneko’s paper, you’ll see how the interactions occurred.
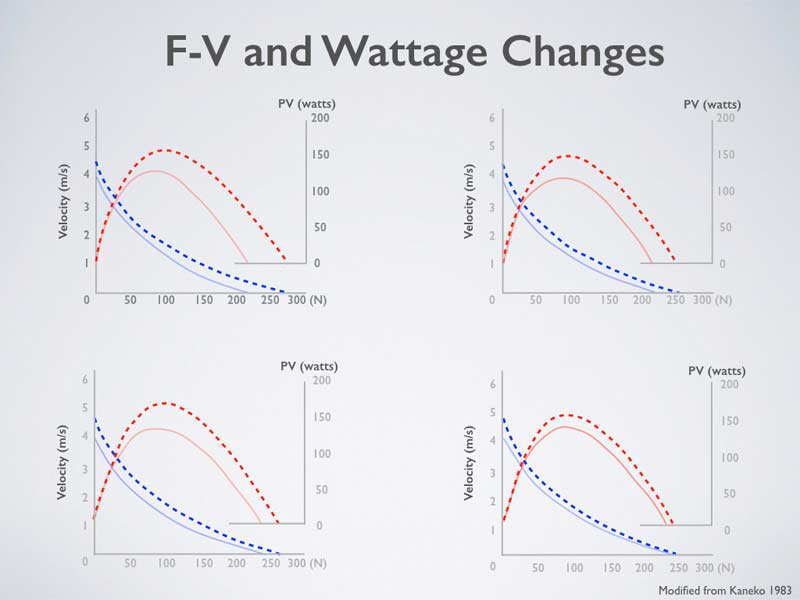
The concave curvilinear lines are force-velocity plots, the convex lines are power-force plots, and both are overlaid onto the same graph. If we look at the training at 100% of 1RM (for squats, dead lifts, and bench presses, this would be absolute strength and circa 0.3 m/s), we see that there was a massive improvement in force and a minimal improvement in velocity. Power did increase significantly, albeit moving to the right slightly. This portion of the chart shows the basis behind Bompa’s statement2 that all strengths relate back to absolute strength—it is obvious that they do. However, the increase in force with no increase in velocity will, over time, cease to show an improvement in power that can be illustrated in the playing arena, as peak power increases do move to the right (indicating that they take longer to achieve).
This adaptation reinforces the findings in the classic graph from Hakkinen and Kraemer’s GSSI 53, where they proposed that maximal strength continually increased force, but the ability to produce force in a short time did not improve.3 The 60% load caused moderate increases in both force and velocity, which led to a power increase going up and only slightly to the right. This sort of balanced training saw a similar increase in power, but it was a result of increasing both force and velocity equally.
This graph illustrates the focus of strength-speed and how both were enhanced through the moderate load, which would be around 0.80 m/s. The 30% load showed a significant increase in velocity and a minimal increase in force, but a great increase in power that went nearly straight up. Great increases in speed and minimal increases in strength show the apropos labeling of speed-strength; these results are achieved at a velocity of about 1.05 m/s on squats and deadlifts (in the speed-strength zone). The 0% load, of course, showed great increases in velocity and very small increases in force. With the imbalance in results, we see that the power increase is small, but it does rise directly above the previous number.
Breaking Down Load and Velocity Further with Profiling
By examining the individual’s load-velocity profile, we can assign them what they need to improve. Is it just force? Do some heavy lifting. If they’re good on force, we can start to improve their power very well by going to strength-speed and utilizing those velocities. If they’ve developed an increase in power by working here, they can move on to speed-strength and utilize those velocities. Only after they have gotten all that they can gain by using speed-strength is it a good idea to use starting strength. You can see here how the adaptations got their names based on what they develop and how.
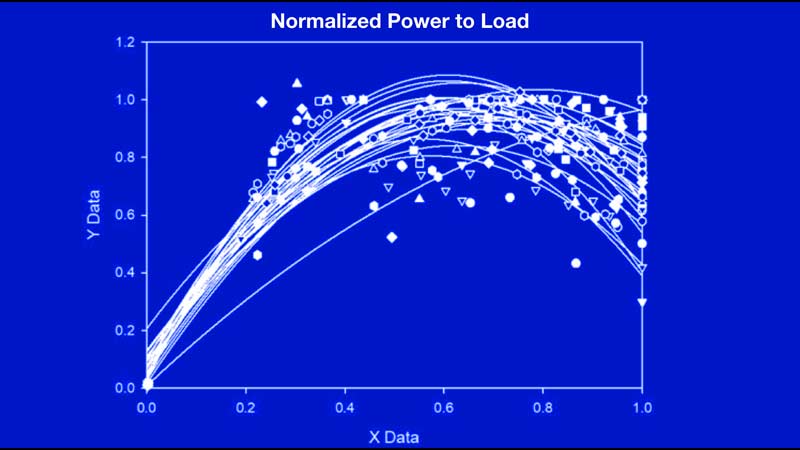
Only after athletes have gotten all that they can gain by using speed-strength is it a good idea to use starting strength, says @jbryanmann. Share on XBelow are two tables showing data we have gotten from high-level Division 1 athletes using the GymAware. The unloaded condition was collected through the use of a PVC pipe and performed as ballistic (i.e., they jumped into the air from the depth of the lift). The first chart is a spaghetti plot illustrating power and where athletes achieve it in relation to their 1RM. This is normalized power to load and has led everyone on the entire team to allow us to make more wide-sweeping decisions. The fact that the plot is normalized means that the loads were based off their 1RM, and their power was based off their maximal power as well.
There is no load greater than 1.0 and no power greater than 1.0. With the information related back to absolute strength, force, and relative velocity, decisions can be made about how to train to enhance power in a more efficient manner. In most instances, weak individuals will improve their power capabilities by simply getting stronger. When someone is strong, they tend to need to utilize faster velocities to cause power to increase.
When examining the data below, we see that most of the athletes achieve peak power at around 60% of 1RM. Some athletes hit peak power at around 40%, and it appears that one athlete hit peak power at 100% of 1RM. The individual who hit peak power at 100% of 1RM actually had poor technique and was not allowed to progress with any greater load, which falsely made him appear to require maximal loads to achieve peak power. I did leave this athlete in for the illustration to demonstrate how this may occur.
The other new “old” thing is utilizing load-velocity profiles for those movements that aren’t the squat, bench, and deadlift. I admittedly had rose-colored glasses on when creating the zones. I looked at this only from my frame of reference with the constraints that were dealt to me by sport coaches and my personal background athletically in powerlifting. They liked certain movements and only wanted those progressed and/or tested. Thus, I never examined stuff outside of the clean, snatch, squat, deadlift, and bench press.
To me, those were the big rock exercises. If it ain’t broke, don’t fix it. This, however, has led to some confusion when trying to apply other exercises, especially those that either have an instability factor or no ground-based component (not even feet touching ground). Of course, these are not going to fall into the same velocities as the squat, deadlift, and bench press—the purpose of the exercise is different.
Load-velocity profiling is basically what everyone does as a result of the Gonzalez-Badillo and Sanchez-Medina paper4. Within a several-week training block, the relative loads at the corresponding velocities are the same, regardless of the changes in the absolute loads. For instance, if someone is stronger for a session, they may be moving 15kg heavier for the same velocity of 0.8 m/s, which happened to equate to 60% of their 1RM. So, you can see how their 1RM is essentially up around 15kg that day, and the converse is true as well.
If the coach happens to collect all of the load-velocity profiles for their important lifts outside of squat and deadlift, they’ll be able to derive their own zones for their exact team by looking for the mean and standard deviations for the velocity at each given percentage. Using their individual load-velocity profile is obviously the most accurate way of training athletes, but if you are beyond a 1:5 ratio, I have found it difficult to maintain this sort of precision and revert back to group means.
Also, you have to continually monitor this. As a result of heavy strength training, you are able to achieve movement at slower and slower velocities as your body has adapted to be able to move these heavier loads. If you look back to that Gonzalez-Badillo study, you will notice that at not one single load were they moving faster—they were moving slower at every intensity. I’ve noticed that athletes seem to drop velocity by about 0.02 to 0.04 m/s per year.
As a result of heavy strength training, you are able to achieve movement at slower and slower velocities as your body has adapted to be able to move these heavier loads, says @jbryanmann. Share on XThis may also be important for athletes of lower qualification but higher strength levels (meaning high school kids who are already performing full squats with greater than two times their body weight with good technique). The zones were collected on a multitude of Division 1 athletes, and sometimes those speeds don’t work for the high school athlete. They don’t have the same nervous system, and you may need to adjust things.
Likewise, for very specific populations like strength-sports—they have gained neuromuscular efficiency to move more slowly to allow them to lift a heavier weight. For instance, my training partner (who is known as Doc Dave, if you have listened to some of the chatter about Westside vs. the World) would achieve a 1RM bench press at about 0.08 m/s, as opposed to the 0.15 m/s that I would see in most Division 1 athletes. Chris Duffin showed a video of him achieving a deadlift at 0.08 m/s, as opposed to the 0.32 m/s I typically saw in most Division 1 athletes.
Load-Velocity Relationships and Further Directions
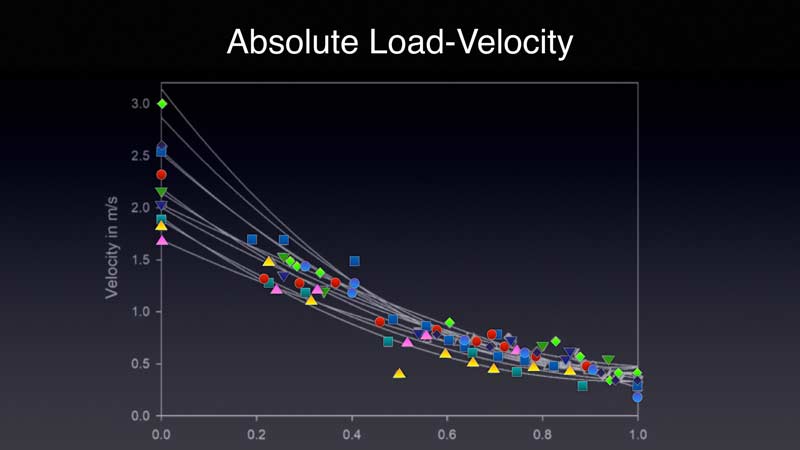
Speaking of the individual load-velocity relationship, below is a load-velocity graph for our athletes, again collected with GymAware. The velocity end of the spectrum was taken with ballistic movements performed on a modified PVC pipe trap bar. The starting position for this was performed at the same height as the high handles with the bumper plates used in the program. We utilized 100% of 1RM as the force end of the spectrum.
By examining the slopes of these curves, we can see if individuals are more deficient in velocity or force. The data plotted are for those who achieved a true 1RM and did not include younger athletes who had difficulty when progressing to heavier loads and dealt with technical breakdowns. These athletes were stopped by the strength and conditioning coach, as their technique was no longer acceptable, and they were thus at a greater risk of injury when continuing with heavier loading.
I do not have normative data as far as what is optimal for load and velocity at this point in time, nor do I have an optimal slope or curve. We do see that there is a pretty significant disparity between those who achieved the highest unloaded velocities and those who achieved the lowest. There was a much smaller discrepancy in loads greater than 60%, and the line became nearly flat after having a slightly curvilinear design with the lighter intensities (less than 40%). It nearly appears as if there are two straight lines that intersect for the velocity and the load ends of the spectrum. With the plethora of data out there showing a curvilinear relationship, we need to collect further collegiate data to examine if this is an issue of the specific population or due to the unconventional nature of examining the entire spectrum of the load-velocity relationship.
I plotted the charts in this article in SigmaPlot due to the fact that I have access to this program and enjoy its capabilities. After a short learning period, the production of various curves was very easy. There are plenty of other programs that can produce data visualizations and will do an excellent job (maybe even better than SigmaPlot). Some people have made gorgeous visualizations even in Excel. Whatever you have access to is what you should use.
To wrap up, these are the two things that I have been looking at lately. While neither is new, if you haven’t heard about it—it’s new to you.
Since you’re here…
…we have a small favor to ask. More people are reading SimpliFaster than ever, and each week we bring you compelling content from coaches, sport scientists, and physiotherapists who are devoted to building better athletes. Please take a moment to share the articles on social media, engage the authors with questions and comments below, and link to articles when appropriate if you have a blog or participate on forums of related topics. — SF
[mashshare]
References
1. Kaneko M, Fuchimoto T, Toji H, and Suei K. “Training effect of different loads on the force-velocity relationship and mechanical power output in human muscle.” Scandinavian Journal of Sports Sciences. 1983; 5:50–55.
2. Bompa, TO and Buzzichelli, Carlo. Periodization: Theory and Methodology of Training. Human Kinetics, Inc., 2018.
3. Hakkinen K, Komi PV, and Alen M. “Effect of explosive type strength training on isometric force- and relaxation-time, electromyographic and muscle fibre characteristics of leg exensor muscles. Acta physiologica Scandinavica. 1985;125:587-600.
4. Gonzalez-Badillo JJ and Sanchez-Medina L. “Movement velocity as a measure of loading intensity in resistance training. International Journal of Sports Medicine. 2010;31:347-352.